Architectural Symbolism of the Scepter

Alexander Ford

Spring, 2022

Introduction

Students of archaic architecture and her traditional symbols will certainly have encountered the notion of the microcosm. For most, it seems satisfactory enough to point out that the temple, in all its forms, is always intended to be emblematic of the world. At the same time there is a companion idea, common to a great many cultures, that the temple is a kind-of corpus or body; the body, as the Biblical saying goes, is a temple. And beyond, there are many traditions to be found which describe the body itself as a microcosmic model, much the same. Though many scholars are happy enough to repeat these associations in passing, in service often times of other goals, a thorough treatment that draws together all three ideas; which sheds a bit of holistic light on the reasoning for the superposition of body, temple, and cosmos itself, remains somewhat elusive.

Of Porphyry’s description of the Mithraic microcosm; the cave of Zoroaster, Thomas Maurice explains:

“... the Mithraic caverns represented the world. According to Eubulus, Zoroaster first of all, among the neighboring mountains of Persia, consecrated a natural cell, adorned with flowers and watered with fountains, in honour of Mithra, the father of the universe. For he thought the cavern an emblem of the world fabricated by Mithra; and in this cave were many geographical symbols arranged with the most perfect symmetry and at certain distances, which shadowed out the elements and climates of the world.”

In an altogether simple way, one may be given to wonder why it was that man of antiquity sought to build his temples in symbolic imitation of the apparent order of the cosmos at all. One may wonder as well how an esoteric understanding of the human body was related to that architectural objective. According to what rationale did the architects of history’s noblest cultures come to draw these same conclusions over, and over again? It remains the case that even the most complex cultural systems established for the architectural modeling of the cosmos must be arranged according to some metaphysical rationale, which, is altogether humane. That is, one which is derived according to a line of thinking that remains evident enough to those who took up the trade, that the persistence of this common, symbolic objective can be seen not as, itself, a doctrine, but rather, as the qualitative fountainhead of architectural doctrines.

At present we will limit the scope to the question of connecting the temple to the body. It seems upon careful consideration that the connection between temple and body is most essentially understood with a discussion of the esoteric symbolism of measurement. From measurement, then, proportion; and from proportion, on to some of the tools and symbols that defined the architect’s qualitative mentality.

Measure

In order to measure something, it must only be related to something else. All that is required for such a comparison to be made (or, that is, for a measurement to be taken) is that the thing being measured shares a quality in common, with the thing being used as a rule. In other words, we can say that to measure one thing is to express it in terms of something else.

In symbolic comparison, we are familiar with the Latin word, ‘ratio,’ but the Greeks named such a statement-of-measure λόγος (logos). Common types of measure—including length, mass, volume, or size—were called μέρος, (meros) or ‘magnitude.’ To the Greek sensibility, magnitude and number were distinguished from one another. The nature of that distinction may not be so immediately clear to the modern observer, and so, in order to properly understand the esoteric importance of concepts like number, proportion, measure—and therefrom, the symbolic character of architectural systems designed according to those concepts—we ought to begin by attempting to clarify this distinction in the Greek mind between a magnitude, and a number.

Take, for example, two lines of arbitrary length—length being a shared quality between them. They can be compared in terms of their length. That they are equal or unequal might be observed, as well as which is longer and which is shorter. These are qualitative judgements, and are inherent to the form of the objects in question. More complex geometric operations can also be performed, which amount to the four basic functions of arithmetic, all entirely without number. Two magnitudes may be appended to produce a sum, one may be removed from another to yield a difference. Two linear magnitudes can be multiplied to form a plane the area of which is their product, and division—that is, the severance of equal components from a whole—can likewise be constructed geometrically, as division is only a form of measurement with a given unit.

A λόγος, or ratio, does two things. It establishes what standard is to be applied as a measuring partition (called the consequent), and it establishes what it is that we intend to measure, or to express in terms of that standard (called the antecedent). That is the simple mystical operation underlying all proportion; the creation of terms of expression has long been a profound, and pervasive occult principle.

The Pythagoreans contended that only if whole, equal components of the antecedent can be measured by the consequent, does the ratio of magnitudes then constitute a number. In that case the given magnitudes are said to be commensurate or, co-measurable. Magnitudes which cannot be expressed as a number in this way are incommensurate. Though an incommensurate thing cannot be defined as a number, it can be expressed as a single, resultant magnitude. The thing exists, but cannot be put to strict language; it can only be demonstrated.

While two magnitudes of different quality cannot be put to a meaningful ratio with one-another, the geometer Eudoxis described a theory of proportion that permitted the comparison of ratios themselves, because, commensurate ratios both constitute numbers (For example, a cone and a cylinder of the same base and height will stand in proportion such that the ratio between their volumes, and the ratio 1:3, are themselves equivalent). All of which is only to say this: Proportion is a constant relationship between ratios, no matter the quality. Proportion, then, as an esoteric concept must be understood to bely a divine governing language, through which, ancient observers were able to glimpse the metaphysical connections, rules, and laws that governed seemingly disparate things.

Man of antiquity used his body as the standard of measurement for all things. The simplest cubit was defined as the magnitude from the elbow to the tip of the fingers. The Greeks observed of their body that four dactyls comprised the width of a palm. A foot was divided as well into dactyls. Larger units of measure were configured from these basic units; a stadion being six-hundred feet, and five-thousand being a mile. Of course there was somewhat little in the way of standardization. It was well known in Ancient Greece that—for example—athletes competing in a footrace in one place, may be running on a slightly longer track than another place, as a foot here was slightly longer than a foot there. Standardization of units themselves is not so important to the discussion of proportion.

To simplify a bit, we might say that because we are men the universe appears to us in terms of man. What it is that we see; what we can grasp through comparison or can measure by computation—those two quarreling twins of all mentality—is necessarily constrained to the terms in which we see. Therefore, the cosmos possesses a fundamentally anthropomorphic quality, because it is man who regards it and passes judgement upon it. Put another way, the hammer sees only a world of things to be struck.

Anaxagoras nodded to the radical, mystical importance of measurement in writing that “the purpose of life is the investigation of the Sun, Moon, and the Heavens.” Further refinement of his propensity for measurement appears, broadly, to be responsible for man’s civilized tendency away from conducting religious rites in wild nature, and toward the design of his own spaces; toward the temple.

Proportion

In the architectural schools today proportion is typically presented in passing, as an aesthetic novelty. It’s something almost frivolous, which is perpetrated upon the architecture according to the superstitious tastes of men who were yet-to-develop a more mature, industrious mentality. Proportion, to the academic, is a matter of antiquated taste, fashion, or style.

That beauty, in the Vitruvian sense of the word, is defined in terms of proportion is known to intellectuals; they are aware of it. The modern intellectual may realize that proportion was a thing of some importance to the ancients, yet, seldom is he able to furnish an explanation for how, or why, which resists materialistic reduction. Of proportion he sees only its mundane, aesthetic aspects. Those over-crude and secularized items, which simply look a certain way, are all that he means when he offers the word. For the intellectual, the word is only a category. Mistaking a manner of making with a manner of looking is perhaps one of the most garish symptoms of modernity.

That one ‘rule’ would be standardized is a materialistic necessity; it serves the tax collector, and the merchant. Conversely, consider that any human body—no matter its individual size relative to another—contains within itself the same rules as any other. That the body expresses certain proportional relationships, in terms of its own λόγος, is always the same. These rules are true, local to any human system. So we understand that a standardized rule is a mundane imposition upon the world, by man. λόγος, by contrast, is a divine formula that characterizes the natural world, and describes the relationships between its constituent parts. This, as well, we can note in passing, is the wellspring of the symbolic accord between the human body and the cosmos for the Ancients; the body is formed according to proportional laws in much the same way that the natural world expresses its own proportional laws. As Vitruvius says,

“…the human body is so designed by nature that the face, from the chin to the top of the forehead and the lowest roots of the hair, is a tenth part of the whole height; the open hand from the wrist to the tip of the middle finger is just the same; the head from the chin to the crown is an eighth, and with the neck and shoulder from the top of the breast to the lowest roots of the hair is a sixth; from the middle of the breast to the summit of the crown is a fourth. … The other members, too, have their own symmetrical proportions, and it was by employing them that the famous painters and sculptors of antiquity attained to great and endless renown.”

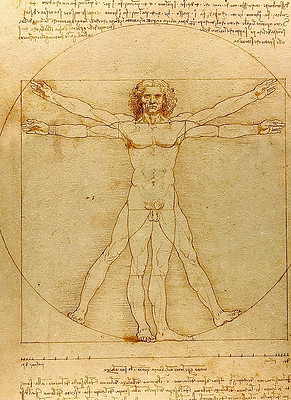
Proportion, we will define as this: Correspondence between the magnitudes of individual parts of a work, and, the correspondence between the entire work and a certain part set out as the rule. Perhaps the most critical proportion evident in the human body, is the squared circle. Vitruvius, again, explains:

“Then again, in the human body the central point is naturally the navel. For if a man be placed flat on his back, with his hands and feet extended, and a pair of compasses centered at his navel, the fingers and toes of his two hands and feet will touch the circumference of a circle described therefrom. And just as the human body yields a circular outline, so too a square figure may be found from it. For if we measure the distance from the soles of the feet to the top of the head, and then apply that measure to the outstretched arms, the breadth will be found to be the same as the height, as in the case of plane surfaces which are perfectly square.”

To attenuate the language a bit, we may say that the body contains within itself a proportional relationship between the square and the circle. Any student of the Hermetic arts will no doubt understand the significance of this observation; that the central symbol of the alchemical opus—the transfiguration of the self; the union between two emblems long-offered to represent the earthly and celestial realms—is contained within, and expressed by the proportional configuration of the human body.

Here we come, at some length, to consider the word itself. When the architects of Ancient Greece spoke or wrote about proportion, of course they did not use the Latin word ‘proportion,’ which was loaned much later into English and passed down to us presently. They used an older, Greek word; one which also still exists in modern English, though, one which for us has lost its architectural connotation: Analogy.

Elsewhere I have commented on the critical role played by philology for any serious esoteric inquiry. On account of shared relevance to the proceeding arguments, I will reproduce that brief passage here, now: ‘It’s hard to justify ignoring the structure of a word or of a name, especially when the object is to interrogate the esoteric intentions of an otherwise hidden subject. Such things are never arbitrary for the ancients, are often idiomatic the further back we can discern their roots, and are seldom categorical. Understanding the literal meaning of a word or a name is invaluable, then, because it reveals what things the ancients who employed those words used, to stand-in for the concepts or ideas they were naming. All are, to some degree, analogies.’

So, to apprehend the Greek idea of proportion as it came to define that architectural tradition, we begin with the word itself. Recall that a ratio was known to the Greeks as ‘λόγος’ (logos). The word for what we call ‘proportion’ in architecture, was ‘ἀναλογία’ (analogia), to the Greeks. Formed by compounding two words, ’ἀνα’ and ‘λόγος,’ we can see even at a glance, that the standard of comparison in sacred geometry, the λόγος, forms the basis of the name the Greeks lent to the system of proportion that governed the temple: Ana-logos.

λόγος descends from the same Proto-Indo-European root as the Latin word ‘legio,’ which is where the modern English word ‘legion’ originates, but which literally meant ‘chosen’ in the Roman tongue; in the military context, something like ‘chosen warriors.’ The Proto-Indo-European root likewise most nearly corresponds to something like ‘to gather up,’ ‘to choose,’ or ‘to collect.’ Heraclitus was the first to apply λόγος as a philosophical principle—signifying those words which are ‘chosen,’ and arranged to physically convey meaning.

‘ἀνά’ (ana-) is typically translated to ‘up.’ However, ἀνά can also translate more nearly to something like the English prefix ‘re-’, as in reuse, remake, or regard. Therefore, ἀνά might be likened, in some cases more accurately, to ‘again.’ In the case of ἀναλογία, it is this second sense, from which I believe the word’s original, literal meaning was formed and lent to the matter of architectural proportion by the Greek masters. In the sense of measurement, ἀναλογία might thus be translated as ‘the standard, again,’ or more nearly, ‘[to take] the standard (λόγος), again.’ Therefore ἀναλογία refers to the process of deriving what-comes-after, given a rule, from what-comes-before. Viewed this way, ἀναλογία is a simple, and literal formation for the act of measurement. Further then—and this is the key—for the ancient architect, proportion by its very name would thus correspond to the reflexive quality of a thing which expresses by virtue of its form, the standard(s) which gives it form.

Perhaps not so well-known is the fact that the Greeks did not employ drawing in their architectural process, to any serious degree. They conducted their architecture in accordance with a canon. The canon was gathered upon a foundation of universal principles. The mechanism of that foundation was proportion. Given several parameters (λόγος), the temple was designed analogically, in-situ, throughout the construction process. Any given state of the system defined the subsequent states. That is what we mean, when we say that proportion is a mystical methodology, not a style; the aesthetic of the proportional method is, itself, incidental.

The Greek architects did not draw largely because it would have been prohibitively difficult to laminate enough individual pieces of parchment, or papyrus, to form a writing surface sizable enough to work to any real degree of detail. Therefore it fell to proportional relationships to lend a measure of predictability to the complex and expensive processes of design, and construction. In order to ensure that the relation between constituent parts remained proportionate, the architect made use of several tools. The exact nature of these tools is not clearly known; we know their names, but not their specific function nor their particular form.

We know that a verbal description of the structure’s dimension and general configuration was common. From that, which is typically called the ‘building account,’ enough was agreed upon between client and architect to begin construction according to the canon. Two tools, peculiar to the architects trade, were called ‘ἀναγραφεύς’ (anagrapheus) not to be confused with the Byzantine bureaucratic office of the same name, and ‘παραδειγμα’ (paradeigma), or paradigm. Broadly speaking, both seem to have been standards of a sort—against which individual components of the temple could be checked and refined by workers and tradesmen, on-site, during construction. A classical sculptor’s pointing-machine comes to mind, comparatively. It is for this reason that the compass, or calipers, are often depicted as the tools of the maker of the universe; the compass allows for a workman to transfer measurements from a divine standard onto a mundane system. They are what permit him to create his temple proportionate to, and therefore in the image of, the world.

Bearing in mind the philosophical implications of proportion to the Greeks, then, consider the following passage from the fifth book of The Histories of Herodotus, where it is said that the architects were able to produce the Temple of Delphi to such a quality as to surpass the paradigm itself:

“After fortifying Lipsydrium north of Paeonia, they [the Athenians], in their desire to use all devices against the sons of Pisistratus, hired themselves to the Amphictyons for the building of the temple at Delphi which exists now but was not there yet then. Since they were wealthy and like their fathers men of reputation, they made the temple more beautiful than the model [παραδειγμα] showed. In particular, whereas they had agreed to build the temple of tufa, they made its front of Parian marble.”

Scepter, and Wand

To locate the scepter and wand symbols in this talk of measure and proportion, we turn our attention now briefly to the Egyptians. Egyptian geometers were able to determine perfect right angles through the use of a twelve-unit cord, according to a rather straightforward process. First the magnitude of a single unit was decided. Next, thirteen knots were tied along the cord so as to partition the length into twelve equal units. The geometer would then fix two foci (rods) at the points following the third, and following the seventh units. With the cord divided then, into lengths of three, four, and five, the leftmost (three) and rightmost (five) segments were rotated around the foci until they intersected at an inevitable point in space. The result is always a proportional triangle—which later came to be given the name of the Greek geometer Pythagoras—as well as a perfect right angle about the first focus. Longer ropes scaled in these proportions could be employed by surveyors on site to establish true axial relationships.

Though not specifically related to the subject at-hand, it’s worth noting at this juncture that the zodiacal importance of the number twelve, and the kheiromantic relevance of the same celestial number represented in the fingers, suggests a deeply-rooted relationship between the symbolism of the hand—that is, its use in divination—and the holy tools of the architect. That discussion, however, is undertaken elsewhere.

The very beginning of the construction process for any sacred structure was the alignment, measurement, and configuration of its foundations. Orienting the foundations was so critically important that the Egyptian architects ritualized the process and gave to it the name “the stretching of the cord.” Alignment to the major, heavenly axis was determined through the use of a sighting rod and careful observation of circumpolar stars. By staking out two lines from the sighting rod, toward the rising and setting of one such star (or several), the astronomer delineated an angle on-site. Bisecting that angle yielded a line of perfect accord to the axis of rotation of the great wheel; true north. From here followed on the major and minor axes of the structure.

The harpedonaptai, as they were named, drew out their cords next, knotted in equal parts to ten units of the structure; ten royal cubits per portion (seven palms of four digits each), and plotted the four corners of the temple. According to this system, the foundation trenches were dug. In them the Pharaoh laid the cornerstones of the temple, and votive offerings were likewise deposited. The ancient sources tell us that the Pharaoh personally took part in the stretching of the cord; tradition holds that he did so together with the goddess Seshat—holding in his hand one rod, and she the other. With golden hammers they staked out the foundations of the microcosm, according to these sacred systems of measurement.

All systems of measure, no matter how complex or primitive—and therefrom all systems of proportion—depend upon the designation of a unit. The unity is quite literally the establishment of the ‘one’ unit of measure, and with a set notion of what one entails, thereafter are determined subsequent valuations. The nature of two is defined in terms of one. Without a sense of what one unit is, it cannot be said that there are two of that thing, or three, and so on.

For early architects the establishment of the unit was an act that permeated the entire structure of the temple, and defined its proportions. Providing the unit is a divining act. As a matter of fact, this line of rationale is very likely the source of the turn of phrase ‘divining,’ as a magical ascertainment. It is well-established, for example, that the intercolumniation (the distance between two columns in the peristyle) was the constraining unit for the Doric temple’s proportional systems, in archaic Greece.

In an esoteric context, it will perhaps now be evident why the act of setting out the unit should be understood as the first cause, which determines and effects the architectural construction. Symbolically, the suppliance of the royal cubit for the construction of the temple therefore is analogous to the cause-without-cause, predicating all of creation. Whereas the geometrical calculations that are conducted by making use of the unit are derived, or perhaps more appropriately determined—in the sense of term-making—given the unit as an axiom, the unity itself is a thing which is conjured up as the case from nothing. It’s not computable. The unit is given, by its nature, from the king according to his intention for the scale of the temple, in the same way that creation is set into its motions according to the impetus of the godhead.

For this reason do many myths the world over describe the creation of the mundane world in terms of a body part of the divine—the body first serving as the paradigm, or model for standards of measurement and exemplary proportions. As we will see in a later discussion, the rationale that apparently links human sacrifice to architectural foundation rituals arises from this manner of thinking as well. The divine body supplies the primum movens for the world (an act which has a necessarily sexual dimension as well), and so too does the human body provide the cubit for the temple, to be made in the manner of the world.

Surveyors and architects have, since the farthest reaches of antiquity, carried in-hand rods of measure. Egyptian and Akkadian cubit rods are among the oldest that survive. Together with the cubit rod, the stake and the knotted cord (which are the true origin of the symbolic rod and ring) constitute the most ancient tools of measurement, and represent the most archaic form of the geometric mysteries. If one studies the iconography of the goddess Seshat, with whom the Pharaoh collaborated the temple foundation rituals, one will find that she carries with her an object that could confidently be interpreted as a staff of measure, and at its base is set the shen; the rod-and-ring emblem.

The exact nature of the royal scepter is thus revealed to be a symbol of the divine will, in the form of the measuring rod. Wielding the scepter represents the king’s sovereignty, for the specific reason that it demonstrates his possession of the divine capacity, or right, to rule. The king’s divine mandate is analogous to the action of the godhead, which provides the prime movement for all of creation—the first cause. It’s not by chance that the English word ‘rule,’ which comes down to us from a distant Proto-Indo-European root, contains the triplicate meanings of measurement, of judgement, and of reign. Turns of phrase like “the rule of law” grow up from the very same analogical root, and even today, we continue to refer to the law itself as having a body, or corpus.

With the scepter, then, serving in a rational way to symbolize sovereignty, unity, and rule, we can at last begin to form a proper understanding of the deeply held and archaic origins of the magic wand, as a symbol for divine creativity. Encapsulated in the wand are all the abilities of transmutation, transfiguration, and transposition; in a word: Creation. It becomes self-evident that both the scepter and the wand as symbols—of the divine provenance of the king, and of the magical arts, respectively—are descendants of the rod of rule. Both owe the Hermetic flowering of their emblematic legacy to the same mysterious architectural seed.

end.